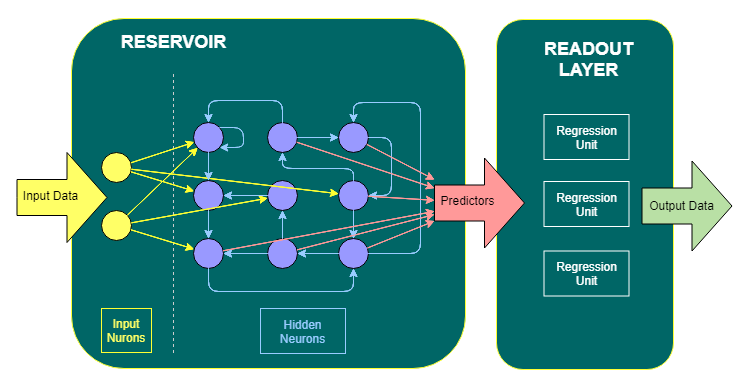
Reservoir computing is a computational framework that is derived from the theory of recurrent neural networks. It maps input signals into higher-dimensional computational spaces using the dynamics of a fixed nonlinear system. This makes it an efficient way of handling a wide variety of complex tasks. In addition to being fast, reservoir computing is also highly flexible.
Liquid state machine (LSM)
Liquid state machine for reservoir computing uses a multiplayer architecture. The reservoir has an input layer and a lower layer that contains LIF neurons and a memory less readout circuit. The reservoir transforms a lower-dimensional input stream into a higher-dimensional one, and the memory less readout circuit uses the results to compute a new value.
A Liquid State Machine (LSM) is a neural model that transforms time-varying inputs to a higher-dimensional space. It consists of three essential parts: the input layer, the reservoir, and the memoryless readout circuit. These three components are important because they allow the machine to achieve its maximum performance in the real-world. Online learning of a LSM is advantageous because it reduces implementation costs. Batch learning can introduce unnecessary complexities.
In deep-LSM, the hidden layers are similar to the liquid layer, with the difference that the connections between the neurons are sparse. The degree of sparsity depends on the application and the number of input signals. The use of granule cells produces a 10-30x increase in dimensionality.
The deep-LSM model uses several deep hidden layers that capture the dynamic behavior of input streams. It also implements attention layers, which reduce the overall synaptic connection. In addition, it uses WTA layers to condense high-dimensional activity into a low-dimensional representation. The WTA layer also reduces the size of the deeper hidden layer, which improves its scalability.
Liquid state machine with bi-stable memristive synapses
The Liquid State Machine (LSM) is a neural network that transforms a stream of input signals into a high-dimensional spatial pattern. This model is based on the idea that the neurons in the brain have their own intrinsic temporal dynamics. This model can be applied to neural networks that are difficult to train.
A typical LSM structure contains an input, a liquid, and sparsely interconnected neurons. In addition, the readout is trained using supervised learning techniques. To further improve the accuracy of the LSM, the number of neurons is increased in a quadratic relationship. However, this approach introduces problems regarding scalability and cost. Another important parameter affecting accuracy is the percentage connectivity. If the connectivity is high, the accuracy will be low.
To study the AP of an LSM, Maass et al. used significantly different examples as training sets. Roy and Basu used jittered versions of ui (). In this way, the AP of a liquid is evaluated using the rank concept. A lower rank indicates that the liquid can generalize better.
A single liquid LSM has lower accuracy than a Nens liquid. It also has lower average accuracy than its counterparts. A dual-liquid LSM has a higher maximum accuracy than a single-liquid LSM. The Nens liquid LSM has a higher average accuracy.
Liquid state machine with recurrent neural network (RNN)
Liquid state machines are recurrently connected nodes that can compute a wide range of nonlinear functions, including speech recognition and computer vision. They use the analogy of a stone falling in a liquid, causing ripples, and convert input into a spatio-temporal pattern of liquid displacement. A key feature of liquid state machines is that they are not hard-coded for a specific task, making them ideal for general-purpose applications.
A liquid state machine is a general-purpose machine-learning model that has many advantages, such as energy efficiency, generalization, and fast training speed. While a Liquid State Machine is ideal for machine-learning applications, it cannot solve complex real-world tasks on its own. For this reason, it is important to use multiple Liquid State Machines together.
LSTM offers considerable benefits in terms of memory savings and operations reduction, compared with the standard LSM. It also offers a significant improvement in classification accuracy, as measured by the classification accuracy on two datasets with a total of 1000 spiking neurons. Compared to LSM, LSTM offers 90% memory savings and a 25% reduction in operations.
Another feature of Liquid State Machine is that it is able to simulate multiple sequential inputs. For example, a simulated input would contain digits 7, 3, 2, and 1. A red box would indicate a response, while a green dashed line would indicate a new input.
The deep-LSM is a computationally efficient model, requiring only a fraction of the compute operations and memory required by other methods. This model can also process input in multiple time-scales. Compared to its shallow counterpart, deep-LSMs can extract more complex temporal features and send them to a readout layer.
Reservoir computing with NG-RC
Reservoir computing can simulate the flow of fluids in a reservoir. The reservoir is represented by a set of continuous-time ordinary differential equations (ODEs). These equations may also include delays incurred along network links. In some cases, the reservoir state is modeled using a linear regression method.
Traditional RC requires a long warm-up time. NG-RC, on the other hand, uses a shorter warm-up period. Traditional RC typically requires 103 to 105 data points. In this way, NG-RC reduces the number of data points required for reservoir computation.
The model can also be trained very quickly and inexpensively, making it a suitable candidate for use in a wide range of physical systems. It can also be applied to classical forecasting methods. Another advantage of reservoir computing is that the training data sets are smaller than for conventional RC. This technique is particularly suitable for learning complex spatio-temporal behaviors.
When training is successful, NG-RC is able to predict the dynamics of a complex dynamical system. This allows reservoir computer implementations to scale very large fields with a single simulation. The computational resources of NG-RC include nonlinear functions and multimodal optical parametric processes. However, the extraction of outputs is challenging in the quantum regime.
The use of reservoir computing with NG-RC in a heterogeneous environment is becoming a more viable option in reservoir exploration. By using nonlinear dynamical systems, reservoir computing is enriched with the addition of a variety of chemical processes. For example, a polyoxometalate molecule in distilled water exhibits exceptional computing power for solving a second-order nonlinear problem.
Reservoir computing with FORCE learning
Reservoir computing is an important technique for the development of machine learning systems. Using a reservoir as a memory, one can learn to model the data in a reservoir by learning from the previous inputs. The information processing capacity of a reservoir is a key concept, since it defines the amount of computation that can be performed. This capacity is related to the stability regime of the reservoir.
Reservoir computing has several advantages. First, the reservoir is a space that can be accessed by the rules of the system. The data in the reservoir can be changed by iterating. This can be accomplished in two ways. The first is to adjust the size of the input vector. The second way is to alter the length of the zero buffer. This allows for reasonable information diffusion over time.
Reservoir computing also provides a method for generating coherent signals from noisy, chaotic data. It is especially useful for learning dynamical systems with complex spatiotemporal behaviors. The neural network output value is calculated from the sum of the input signals. The value of the input is transformed into an output signal using an algorithm called FORCE learning.
Reservoir computing is easy to evaluate, and the quality of the reservoir can be measured before the learning task is chosen. There are several task-agnostic metrics for evaluating the reservoir, such as the memory capacity and the nonlinear information processing capacity. This will help in making the best decision as to which learning task to use.
Another advantage of reservoir computing is that the reservoir computing framework is extendible to Deep Learning. It allows for efficient training of temporal and recurrent neural networks. The Deep Echo State Network (DeepESN) model is a good example of this. It enables researchers to understand the layered composition of recurrent neural networks.